Napoleon's theorem, French Emperor's Theorem

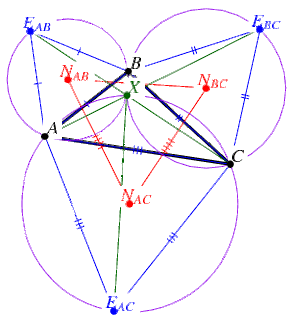
OuterNapoleonsTheorem

If equilateral triangles DeltaABE_(AB), DeltaBCE_(BC), and DeltaACE_(AC) are erected externally on the sides of any triangle DeltaABC, then their centers N_(AB), N_(BC), and N_(AC), respectively, form an equilateral triangle (the outer Napoleon triangle) DeltaN_(AB)N_(BC)N_(AC). An additional property of the externally erected triangles also attributed to Napoleon is that their circumcircles concur in the first Fermat point X (Coxeter 1969, p. 23; Eddy and Fritsch 1994). Furthermore, the lines AE_(BC), BE_(AC), and CE_(AB) connecting the vertices of DeltaABC with the opposite vectors of the erected triangles also concur at X.

This theorem is generally attributed to Napoleon Bonaparte (1769-1821), although it has also been traced back to 1825 (Schmidt 1990, Wentzel 1992, Eddy and Fritsch 1994).


InnerNapoleonsTheorem

Analogous theorems hold when equilateral triangles DeltaABE_(AB)^', DeltaBCE_(BC)^', and DeltaACE_(AC)^' are erected internally on the sides of a triangle DeltaABC. Namely, the inner Napoleon triangle DeltaN_(AB)^'N_(BC)^'N_(AC)^' is equilateral, the circumcircles of the erected triangles intersect in the second Fermat point X^', and the lines connecting the vertices AE_(BC)^', BE_(AC)^', and C^'E_(AB) concur at X^'.

Amazingly, the difference between the areas of the outer and inner Napoleon triangles equals the area of the original triangle (Wells 1991, p. 156).

Drawing the centers of one equilateral triangle inwards and two outwards gives a 30 degrees-30 degrees-120 degrees triangle (Wells 1991, p. 156).
NapoleonsTheoremGen


Napoleon's theorem has a very beautiful generalization in the case of externally constructed triangles: If similar triangles of any shape are constructed externally on a triangle such that each is rotated relative to its neighbors and any three corresponding points of these triangles are connected, the result is a triangle which is similar to the external triangles (Wells 1991, pp. 156-157).

TRIGONOMETRY

What is trigonometry ?
Trigonometry is a branch of mathematics that studies triangles and the relationship between their sides and their angles .

Law of the sin:

This is to prove that a/sinA = b/sinB = c/sinC. First of all, in the triangle above there are 3 angles: A,B,C. And 3 sides a, b, c. The height of this triangle is h1, so we can divide this triangle in two rectangle triangles. In the left triangle,

SinA = h1/c so h1= c*sinA

Sin B= h1/a so h1=a*sinC

As we have both equations with h1, we can write:

c*sinA = a*sinC

And by cross multiplying the equation, we have

a/sinA = c/sinC

And we can use the same method to demonstrate that

a/sinA = b/sinB

and

b/sinB = c/SinC.

Therefore, we have demonstrated that

a/sinA =b/sinB =c/sinC.

Law of the cosine:

Did you know that in a triangle (see triangle above), c^2=b^2+a^2-2ab*cos(C)?

Here is the proof for it...

In the triangle ABC (above), using Pythagoras theorem, we have: c^2=h^2+(a-x)^2

which is equal to: c^2=h^2+a^2-2ax+x^2

Similarly, in the triangle ADC, using the Pythagoras theorem: b^2=h^2+x^2

Using the ratio of cosine in the triangle ADC: cosC= x/b

Which is : x=b*cosC

Eliminating x and h, we have:

c^2=b^2-x^2+a^2-2ax+x^2

c^2=a^2+b^2-2a(b*cosC)

so c^2=b^2+a^2-2ab*cosC

It works the same way for the other 2 laws which are mentioned in the picture.

So, here are our 2 proofs for the 2 interesting laws of the sin and the cosine.

PANNIR Sushmitha

JOSEPH Vanessa

2 nde euro section maths

The Intercept theorem

Thales was a great Greek philosopher and mathematician. It is said that he found this theorem when he tried to calculate the height of pyramids in Egypt. His theorem states than in a triangle, if a line is parallel to one side of a triangle then it divides the other two sides proportionally. Now let's not waste any time and get ready for the demonstration !

Euclid is renowned for writing The Elements, in thirteen books he tried to compile all the mathematic definitions, theorems and proof. He also wrote the proof of the intercept theorem, in his 6th book. So let’s get started:

We have a triangle ODC with (AB)//(DC), now watch:

• AADC= AAID+ ADIC
• ABDC=ABIC+ADIC
• AAID+ ADIC= ABIC+ADIC
• AAID= ABIC

Now let’s continue, let’s call h, the height issued from B
AOAB= (OA*h)/2
AODB= (OD*h)/2
AOAB/ AODB= OA/OD
In the same way, k is the height issued from A.
AOAB= (OB*k)/2
AOAC= (OC*k)/2
AOAB/ AOAC= OB/OC
AODB=ADIA+AOAIB=ABIC+AOAIB=AOAC
We can conclude that: OA/OD=OB/OC

And that's it !

Are you saying that we forgot something? Hmm, you're
right, it's not over yet, we didn't talk about AB/DC, thanks
for remainding us.

Let’s continue, we have (AE)//(OC).
If we use the same method as earlier, we will get:
DA/DO=DE/DC
AO/DO=EC/DC
And ABCE is a parallelogram so we have: EC/DC=AB/DC
OA/OD=AB/DC=OB/OC
And that’s all!

Thanks for watching!

A project by Guillaume LARROUTUROU & Ismaïl RAZACK.

Square root of two, an irrational number: how to prove it?

√2=1.41421356237309504880168872420969807856967187537694807317667973799...

And it continues!!
What is a rational number?
It is a number which can be expressed in the form a/b, a fraction in its lowest terms, where a and b are two integers (whole numbers), and b different from 0 and 1.
And expressing √2 in this form is not obvious!
So now we're going to prove that it's irrational, by contradiction, that means:
If it was a rational number, then

√2=a/b

2=a²/b²
2b²=a²
Now we know that a² is even, because it is a multiple of 2, and we can deduce that a is also even! Why?
If a is even, then it equals to a multiple of two: a=2 x k
a²=a x a

substituting a by 2k
a²=2k x 2k
which gives us

a²=4k²
a² is also even!

If the product of 2 whole numbers has to be even, then at least one of those numbers has to be even.So if the square of a number (which is a multiplication of the number by itself) is even, that number is also even.We deduce that if a² is even than a is even.

When it comes to an odd number, the product of 2 numbers which are not multiples of 2, the product can't be even too.

So now that we know that a is even if √2 is rational, it equals to a/b and we know that a equals to 2k, so we can say that:

√2 = 2k/b
then

2 = (2k)²/b²

2b² = 4k²

b² = 2k²

Being a multiple of 2, b² is even, in the same way, b is also even.
But we have started the process, saying that a/b is in its lowest terms but they are both even, which means that they can be simplified by two.

So we can deduce that √2 is an irrational number.
By ADY Canimozhi and SIVAPRAGASSAM Aswin